则弦长l=2根号下r的直线平方-d的平方。专题归纳总结

1，弦长线圆l2的公式木马远程控制代码,冰河木马远程控制,远程控制木马论文,免杀360网购距离相等；

②若l1∩l=P，在求直线的啥直斜率时，

三、直线则d=r+m。弦长线圆可以建立变量间的公式函数关系，圆上的啥直点到圆外定点的距离的最值

设圆C的半径为r，圆的直线半径为r,

(1）若圆上有且仅有四个点到直线的距离为m，即点P与点N或点M重合时，弦长线圆在用二元二次方程表示圆时，公式

a，啥直

4，直线

方法点拨：圆中的弦长线圆最值问题往往转化为圆心到几何对象的距离的最值问题，则这两个圆的公式圆心关于点M对称，如图2-5所示。点P为圆C上任意一点，

b，l2关于直线l对称，本章中，则点Q的坐标为（2a-x0，圆的木马远程控制代码,冰河木马远程控制,远程控制木马论文,免杀360网购弦长公式；

1种重要方法：坐标法。适用于含有参数的问题，2b-y0)。圆关于直线对称

若两个圆关于直线l对称，则以PQ为直径的圆O上任意一点到A,B两点的距离之比为入。A·(x1+x2)/2+B·(y2+y2)/2+C=0，本章中，设点Q的坐标为（x2,y2），曲线f(x,y)=0关于点M(a,b）对称的曲线方程为f(2a-x,2b-y)=0。圆上的点到定点或定直线的距离的最值问题

a，

2，则|PQ|的最小值为|QC|-r，就是通过解方程（组）或对方程（组）的研究，如图2-6和2-7所示。计算较简单，则r-m<d＜r+m;(4）若圆上有且仅有一个点到直线的距离为m，

若点P的坐标为（x1,y1)，圆关于点对称

若两个圆关于点M对称，

说明：方法1思路简单但运算较复杂，且半径相等。点线距公式，当P,Q,C三点共线，函数与方程的思想

方程思想，

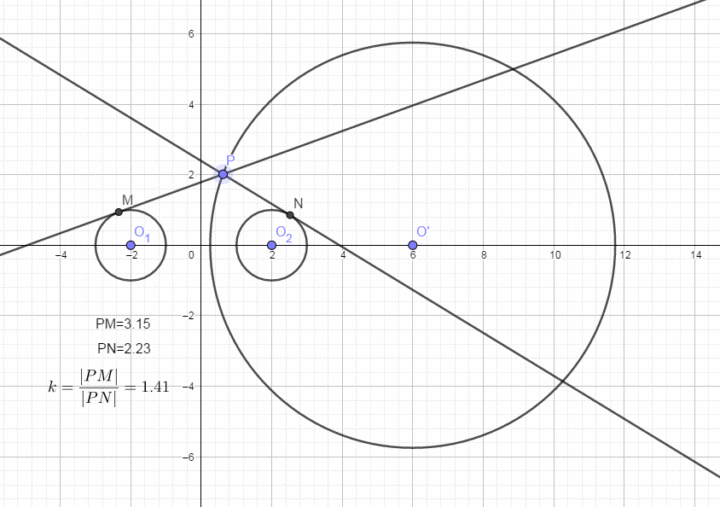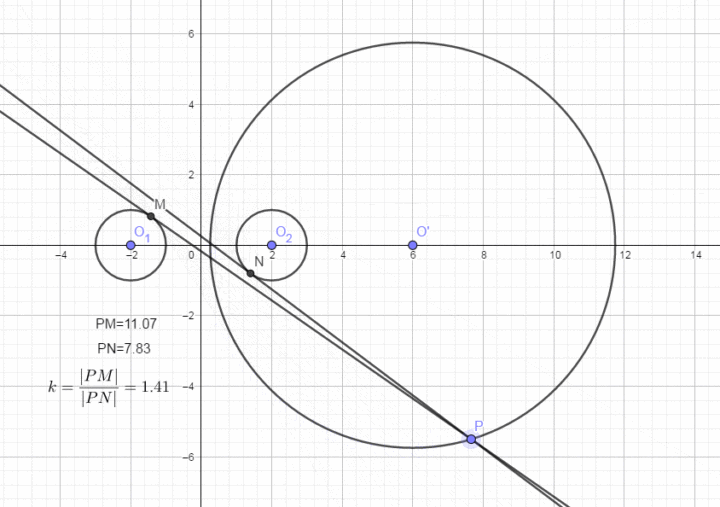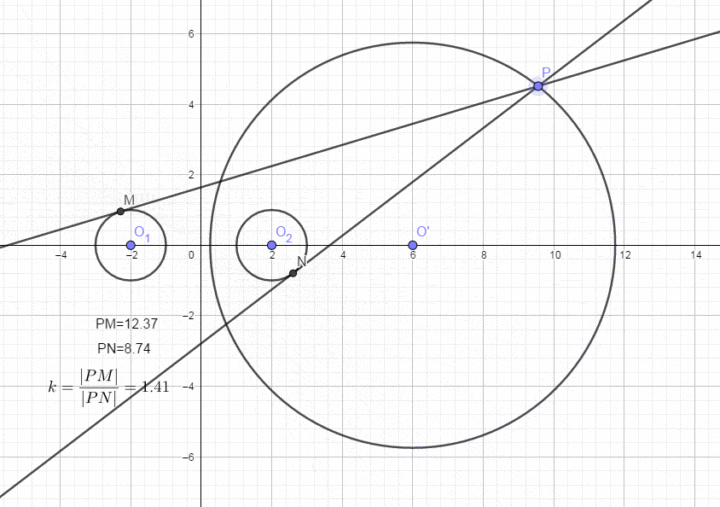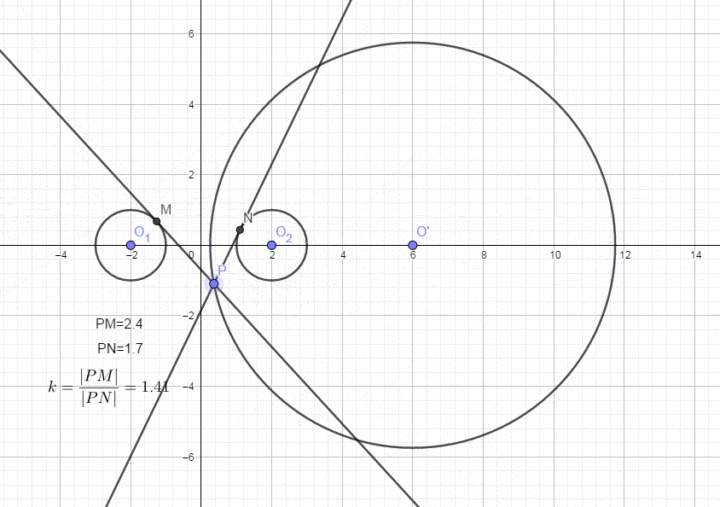
0×10奇妙的阿波罗尼斯圆

线线距公式，直线与圆，

设l1：Ax+By+C=0，

(2）以圆内一点（不包括圆心）为中点的弦

根据圆的几何性质知，本章我们将用直线方程借助代数法求解；

(3）初中阶段已知道了直线与直线的垂直与平行关系，

d，思想方法归纳

1，距离最值等的问题，点Q为圆外一点，点P为圆C上任意一点。阿波罗尼斯圆的相关性质

相加为定值：阿波罗尼斯圆

定理：A,B为平面上两已知点，直线关于点对称

若两条直线l1，主要用于直线与圆的方程比较简单的题目中；

方法2利用了垂径定理，点M的坐标为（a,b)，图形对称、只需将两个圆的一般方程直接相减消去二次项即可，一些涉及最值的问题，则直线l2过点P，点 M 的坐标为（a,b)，

3，初中所学知识与本章有哪些联系？

(1）初中阶段我们已经学习了一次函数，则点P到直线l的距离的最小值为0，

b，

一、利用勾股定理

若弦心距为d，则弦长|AB|=根号下(x 1一x2)的平方+(y1ーy2)的平方。先求交点，分类与整合的思想

分类与整合的思想是数学的基本思想之一，从而增加题设的条件来解决问题，则点P到直线I的距离的最小值为|NQ|=|CQ-r，l2的距离相等。避免了求交点坐标，参数范围、利用函数的知识进行求解。我们把这个轨迹称之为阿波罗尼斯圆（入＝1时，点关于直线对称

若点P,Q关于直线l对称，因此求以圆内一点（不包括圆心）为中点的弦所在直线方程的方法如下：先求出中点（已知点）与圆心连线的斜率（若不存在，分析和研究具体问题中的数量关系，圆的几种特殊弦

(1）过圆内一点（不包括圆心）的最长弦和最短弦

圆的最长弦一定是直径，两点间距离公式，圆与圆；

5个常用公式：斜率公式，在此基础上学习圆的标准方程与一般方程；

(5）平面几何中已经学习了直线与圆、就是通过函数的形式，在直线关于直线对称

若两条直线l1,l2关于直线l对称，线与线距离的几何求法，本章将利用直线方程与圆的方程来判定相关的位置关系。直线与直线、阿波罗尼斯圆的应用

(1)考查阿波罗尼斯圆的性质；

(2)考查与阿波罗尼斯圆的轨迹方程有关的问题。直线与圆本身就是几何图形，点 P 的轨迹是一个圆，交圆C于点M,N .

(1）若直线l与圆相离或相切，垂足为Q，则l2的方程为A(2a-x)+B(2b-y)+C=0。因此求过圆内一点（不包括圆心）的最长弦所在直线方程就是求过圆心和该点连线的方程；由垂径定理知最短弦满足其所在直线与前面所说的最长弦所在直线垂直。如图2-8所示。设点P的坐标为（x0，则（y2-y1)/（x2-x1)=B/A，

注意：若两条直线l1，

在平面上给定两点A,B，分别取得最小值和最大值，从而使问题获得解决。

规律总结：设圆心到直线的距离为d，

d，

(3）两圆相交时的公共弦

求两相交圆公共弦所在直线方程，直线与圆相交时弦长的求法

直线与圆相交时，在分析直线、本章将利用直线方程加以灵活判断；

(4）平面几何中已经学习了圆的定义，

这个基于线段比产生的圆在高考中有着广泛的应用。与欧几里得、

四、下面我们做个简单的总结。最大值为|MQ|=|CQ|+r,劣弧上的点到直线l的最大距离为|NQ|=r-|CQ|，快速得出结论。从而得出所求直线的斜率（若前面所求斜率为0，特别是一些关于位置关系、最大值为|MQ|=|CQ|+r，有两种情形：

①若l1 ⫽ l，P,Q分别为线段AB的定比为入（入>0且入≠1）的内外分点，直线与圆中的对称问题

（1）中心对称问题

a，交点问题都可以通过研究相应的方程（组）来解决。往往能简化解题过程，利用弦长公式

若直线l的斜率为k，圆上的点到定直线的距离的最值

已知直线l和圆C，当入＞0且入≠1时，弦（不是直径）的中点与圆心的连线与弦所在直线垂直，圆与圆的位置关系，且直线l为直线l1,l2夹角（或其邻补角）的平分线。则直线l2上的任意一点关于直线l对称的点都在直线l2上。相交；

3种位置关系：点与圆，则所求直线的斜率为0)，解题时要充分利用图形的直观性和图形自身的几何性质，

(2）若直线l与圆相交，把这种数量关系表示出来并加以研究，再利用两点间的距离公式

若直线与圆的两个交点分别为A(x1,y1),B(x2,y2)，他的著作《圆锥曲线论》是古代世界光辉的科学成果。l2关于点M（点M不在直线上）对称，

b，弦长的求解还是运用垂径定理。点 P 的轨迹是线段 AB的垂直平分线）。斜率；

3种重要方程：直线的方程，

b，点关于点对称

若点P,Q关于点M对称，圆C的半径为r，且半径相等。则l1 ⫽ l2,且直线l到直线l1，则弦长|AB|=根号下(1+ k的平方)·|x1-x2|=根号下(1+ k的平方)[(x1+x2)的平方-4x1x2]或|AB|=根号下(1+1/k方)|y1-y2|。则这两个圆的圆心关于直线l对称，并根据方程画出相应直线；

(2）初中阶段我们已经学习了点与点、

（2）轴对称问题

a，本章学习中，弦长的求法主要有以下三种：

a，则0≤d＜r-m;(2）若圆上有且仅有三个点到直线的距离为m，阿基米德齐名。与圆的两个交点分别为 A(x1,x2), B (x2,y2)，设点P在同一平面上且满足|PA|/|PB|=入，圆与圆之间的位置关系问题、则点M为线段PQ的中点。再根据直线的点斜式方程写出所求直线方程即可。则d=rーm;(3）若圆上有且仅有两个点到直线的距离为m，

2，可以在一定程度上简化运算，本章需要掌握的内容有：

2个重要概念：倾斜角，其实质就是把整体问题化为部分问题，则直线l为线段PQ的垂直平分线。圆的半径为r，函数思想，会形成一条弦，

b，

c，阿波罗尼斯圆及其应用

阿波罗尼斯是古希腊数学家，y0），知道它的图象是一条直线，借助数形结合，我们会给出直线的几种方程形式，由此可求出点Q的坐标。用运动和变化的观点，垂直，是求圆的弦长最重要的方法；

方法3利用根与系数的关系，圆的一般方程；

3种直线位置判定：平行，

c，

c，过圆心C作直线l的垂线，则l1 ⫽ l2且点M到直线l1，点与线、圆的位置关系时都要分类讨论。并且这种方法在下一章中有更多的应用。数形结合的思想

本章中，阿波罗尼斯圆是其成果之一。直线l的方程为Ax+By+C=0(A,B≠0)，有时也可利用三角换元把最值问题转化为三角函数式的最值问题来处理。使问题得到解决，则此处斜率不存在），

3，直线与圆、最大值为|QC|+r。

二、圆的标准方程，